Difference between revisions of "Model concepts"
m |
m (→Model concepts) |
||
| Line 9: | Line 9: | ||
| | | | ||
== Model concepts == | == Model concepts == | ||
| − | Model concepts of different complexity | + | Model concepts of different complexity can be used for the modeling of flow and transport in fractured porous media. Here is an overview of the major groups. |
[[File:EPM_square.png|x200px|Equivalent porous medium approach.|frameless|right|Equivalent porous medium approach.]] | [[File:EPM_square.png|x200px|Equivalent porous medium approach.|frameless|right|Equivalent porous medium approach.]] | ||
| Line 16: | Line 16: | ||
The equivalent porous medium model is a standard model concept for porous media with parameters averaged over control volumes. | The equivalent porous medium model is a standard model concept for porous media with parameters averaged over control volumes. | ||
Usually, a flow model and a transport model are solved. | Usually, a flow model and a transport model are solved. | ||
| − | The flow field can be computed | + | The flow field can be computed based on Darcy's law. |
The contaminant transport is described by the advection-dispersion equation, where different processes like sorption and degradation can be included. | The contaminant transport is described by the advection-dispersion equation, where different processes like sorption and degradation can be included. | ||
Due to its simplicity and its low computational effort, the EPM model is widely used, also for fractured geologies. | Due to its simplicity and its low computational effort, the EPM model is widely used, also for fractured geologies. | ||
| − | + | Fractures, however, are not explicitly modeled. | |
Instead, bulk hydraulic conductivities and effective diffusion or dispersion coefficients are used. | Instead, bulk hydraulic conductivities and effective diffusion or dispersion coefficients are used. | ||
This has as consequence that flow and transport in fractures and the exchange with the matrix cannot be correctly reproduced, leading to poor predictions for transport in dual-continuum aquifers. | This has as consequence that flow and transport in fractures and the exchange with the matrix cannot be correctly reproduced, leading to poor predictions for transport in dual-continuum aquifers. | ||
| Line 29: | Line 29: | ||
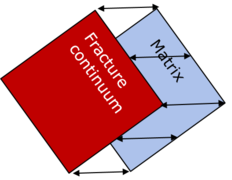
The dual-continuum model, often also called dual-porosity model, uses two continua, the matrix and the fracture continuum. | The dual-continuum model, often also called dual-porosity model, uses two continua, the matrix and the fracture continuum. | ||
Balance equations for flow and transport are formulated for each continuum, and the two continua have the same dimensionality (e.g. 3D fracture continuum and 3D matrix continuum). | Balance equations for flow and transport are formulated for each continuum, and the two continua have the same dimensionality (e.g. 3D fracture continuum and 3D matrix continuum). | ||
| − | |||
| − | |||
The continua are coupled via exchange fluxes using the source and sink terms in the balance equations, allowing for exchange of water and substances between fractures and matrix. | The continua are coupled via exchange fluxes using the source and sink terms in the balance equations, allowing for exchange of water and substances between fractures and matrix. | ||
| − | For that purpose, | + | For that purpose, exchange coefficients have to be specified, which determine the exchange fluxes between fracture and matrix continuum. |
The exchange coefficients are usually used as fitting parameters. | The exchange coefficients are usually used as fitting parameters. | ||
| − | Concepts with more than two continua | + | The basic concept is described in Gerke and Van Genuchten (1993). |
| + | Different parameters are used in the two continua, f.e. porosities and conductivities specific for the fractures and for the matrix. | ||
| + | Concepts with more than two coupled continua have also been developed, f.e. the Multiple INteracting Continua approach (MINC). | ||
<br clear=all> | <br clear=all> | ||
| Line 41: | Line 41: | ||
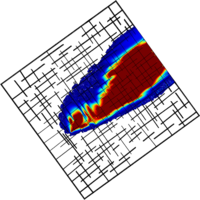
The discrete-fracture model (DFM) is the most detailed approach for fracture flow and transport modeling. | The discrete-fracture model (DFM) is the most detailed approach for fracture flow and transport modeling. | ||
The (major) fractures are explicitly discretized and embedded in the porous matrix. | The (major) fractures are explicitly discretized and embedded in the porous matrix. | ||
| − | + | Fractures and matrix are coupled at the fracture-matrix interface by flux continuity and continuity of the primary variables (hydraulic head, concentration). | |
| − | + | This is the most physically-based approach and the exchange between fractures and matrix is calculated by the model. | |
| − | Fractures and matrix are | ||
| − | This is the most physically-based approach and the exchange between fractures and matrix | ||
However, the numerical efforts are also highest for this model, especially for complex fracture networks with many fractures. | However, the numerical efforts are also highest for this model, especially for complex fracture networks with many fractures. | ||
| − | For good simulation results, a very fine grid resolution at the fracture-matrix interface is | + | For good simulation results, a very fine grid resolution at the fracture-matrix interface is essential. |
| + | |||
| + | Usually, the fractures are resolved with one dimension less than the matrix (e.g. matrix is a 3D volume while the fractures are 2D planes). | ||
| + | The geometric properties of the fractures have to be specified by properties like aperture, length, spacing, main orientation. | ||
| + | The parallel-plate model and the cubic law are often used to describe the flux and the velocity in fractures. | ||
| + | This means, that the fracture is considered as the flow between two parallel plates (without roughness). | ||
| + | The cubic law gives a link between fracture aperture and fracture conductivity (and hence the fracture flux). | ||
| + | It scales the fracture flux with the aperture cubed, hence large-aperture fractures have significantly higher fluxes than fractures with a small aperture. | ||
[[File:Plume DFM 8yrs highKcontrast-50ug.png|x200px|none|thumb|Example of a transport simulation with a DFM showing PCE concentrations.]] | [[File:Plume DFM 8yrs highKcontrast-50ug.png|x200px|none|thumb|Example of a transport simulation with a DFM showing PCE concentrations.]] | ||
Revision as of 18:53, 29 January 2018
| Highlights |
|---|
|
ContentsModel conceptsModel concepts of different complexity can be used for the modeling of flow and transport in fractured porous media. Here is an overview of the major groups. Equivalent porous-medium model (EPM)The equivalent porous medium model is a standard model concept for porous media with parameters averaged over control volumes. Usually, a flow model and a transport model are solved. The flow field can be computed based on Darcy's law. The contaminant transport is described by the advection-dispersion equation, where different processes like sorption and degradation can be included. Due to its simplicity and its low computational effort, the EPM model is widely used, also for fractured geologies.
Fractures, however, are not explicitly modeled.
Instead, bulk hydraulic conductivities and effective diffusion or dispersion coefficients are used.
This has as consequence that flow and transport in fractures and the exchange with the matrix cannot be correctly reproduced, leading to poor predictions for transport in dual-continuum aquifers.
Dual-continuum modelThe dual-continuum model, often also called dual-porosity model, uses two continua, the matrix and the fracture continuum.
Balance equations for flow and transport are formulated for each continuum, and the two continua have the same dimensionality (e.g. 3D fracture continuum and 3D matrix continuum).
The continua are coupled via exchange fluxes using the source and sink terms in the balance equations, allowing for exchange of water and substances between fractures and matrix.
For that purpose, exchange coefficients have to be specified, which determine the exchange fluxes between fracture and matrix continuum.
The exchange coefficients are usually used as fitting parameters.
The basic concept is described in Gerke and Van Genuchten (1993).
Different parameters are used in the two continua, f.e. porosities and conductivities specific for the fractures and for the matrix.
Concepts with more than two coupled continua have also been developed, f.e. the Multiple INteracting Continua approach (MINC).
Discrete-fracture model (DFM)The discrete-fracture model (DFM) is the most detailed approach for fracture flow and transport modeling. The (major) fractures are explicitly discretized and embedded in the porous matrix. Fractures and matrix are coupled at the fracture-matrix interface by flux continuity and continuity of the primary variables (hydraulic head, concentration). This is the most physically-based approach and the exchange between fractures and matrix is calculated by the model. However, the numerical efforts are also highest for this model, especially for complex fracture networks with many fractures. For good simulation results, a very fine grid resolution at the fracture-matrix interface is essential. Usually, the fractures are resolved with one dimension less than the matrix (e.g. matrix is a 3D volume while the fractures are 2D planes). The geometric properties of the fractures have to be specified by properties like aperture, length, spacing, main orientation. The parallel-plate model and the cubic law are often used to describe the flux and the velocity in fractures. This means, that the fracture is considered as the flow between two parallel plates (without roughness). The cubic law gives a link between fracture aperture and fracture conductivity (and hence the fracture flux). It scales the fracture flux with the aperture cubed, hence large-aperture fractures have significantly higher fluxes than fractures with a small aperture.
Random-walk methods |