Difference between revisions of "Model concepts"
(Added some description from the report) |
m (→Model concepts) |
||
| Line 1: | Line 1: | ||
== Model concepts == | == Model concepts == | ||
| − | For the modeling of flow and transport in fractured porous media, | + | For the modeling of flow and transport in fractured porous media, model concepts of different complexity have been developed. Here is an overview of the major groups. |
=== Equivalent porous-medium model (EPM) === | === Equivalent porous-medium model (EPM) === | ||
| − | The equivalent porous medium model is a basic model concept | + | The equivalent porous medium model is a basic model concept with parameters averaged over control volumes. |
| − | |||
| − | |||
Due to its simplicity and its low computational effort, the EPM model is widely used. | Due to its simplicity and its low computational effort, the EPM model is widely used. | ||
| − | + | Usually, a flow model and a transport model are solved. | |
| − | Darcy's law | + | The flow field is usually computed with the help of Darcy's law. |
| + | Fractures are not explicitly modeled, instead they are accounted for in a bulk or average hydraulic conductivity. | ||
| + | However, transport and exchange between fractures and matrix cannot be correctly reproduced. | ||
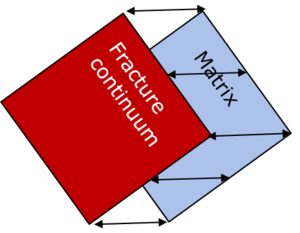
=== Dual-continuum model === | === Dual-continuum model === | ||
| − | A dual-continuum model uses two | + | A dual-continuum model uses two coupled continua. |
| + | One continuum refers to the matrix and the other one to the fracture system. | ||
| + | The basic concept is described in Gerke and Van Genuchten (1993). | ||
| + | Balance equations for flow and transport are formulated for each continuum. | ||
| + | Different parameters are used in the continua, f.e. porosities and conductivities specific for the fractures and for the matrix. | ||
| + | The continua are coupled via exchange fluxes in the source and sink terms, allowing for exchange of water and substances. | ||
| + | The quantification of these exchange fluxes is usually non-trivial. | ||
| + | Concepts with more than two continua (f.e. Multiple INteracting Continua approach, MINC) have also been developed. | ||
[[File:DualContinuumSchematics.png|Dual continuum approach.|none|thumb|Dual continuum modeling approach.]] | [[File:DualContinuumSchematics.png|Dual continuum approach.|none|thumb|Dual continuum modeling approach.]] | ||
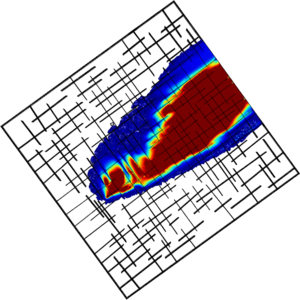
=== Discrete-fracture model (DFM) === | === Discrete-fracture model (DFM) === | ||
The discrete-fracture model (DFM) is the most detailed approach for fracture flow and transport modeling. | The discrete-fracture model (DFM) is the most detailed approach for fracture flow and transport modeling. | ||
| − | + | The (major) fractures embedded in the porous matrix are explicitly discretized. | |
Usually, the fractures are resolved with one dimension less than the matrix (e.g. matrix in 3D, fractures in 2D). | Usually, the fractures are resolved with one dimension less than the matrix (e.g. matrix in 3D, fractures in 2D). | ||
| − | The fractures have to be characterized by properties like aperture, | + | The fractures have to be characterized by properties like aperture, length, spacing, main orientation. |
Fractures and matrix are usually coupled at the fracture-matrix interface by flux continuity and continuity of the primary variables (hydraulic head, concentration). | Fractures and matrix are usually coupled at the fracture-matrix interface by flux continuity and continuity of the primary variables (hydraulic head, concentration). | ||
| + | This is the most physically-based approach | ||
[[File:Plume DFM 8yrs highKcontrast-50ug.png|none|thumb|Example of a DFM simulation.]] | [[File:Plume DFM 8yrs highKcontrast-50ug.png|none|thumb|Example of a DFM simulation.]] | ||
| + | |||
| + | === Random-walk methods === | ||
Return to [[Content]] | Return to [[Content]] | ||
Revision as of 15:31, 3 January 2017
Contents
Model concepts
For the modeling of flow and transport in fractured porous media, model concepts of different complexity have been developed. Here is an overview of the major groups.
Equivalent porous-medium model (EPM)
The equivalent porous medium model is a basic model concept with parameters averaged over control volumes. Due to its simplicity and its low computational effort, the EPM model is widely used. Usually, a flow model and a transport model are solved. The flow field is usually computed with the help of Darcy's law. Fractures are not explicitly modeled, instead they are accounted for in a bulk or average hydraulic conductivity. However, transport and exchange between fractures and matrix cannot be correctly reproduced.
Dual-continuum model
A dual-continuum model uses two coupled continua. One continuum refers to the matrix and the other one to the fracture system. The basic concept is described in Gerke and Van Genuchten (1993). Balance equations for flow and transport are formulated for each continuum. Different parameters are used in the continua, f.e. porosities and conductivities specific for the fractures and for the matrix. The continua are coupled via exchange fluxes in the source and sink terms, allowing for exchange of water and substances. The quantification of these exchange fluxes is usually non-trivial. Concepts with more than two continua (f.e. Multiple INteracting Continua approach, MINC) have also been developed.
Discrete-fracture model (DFM)
The discrete-fracture model (DFM) is the most detailed approach for fracture flow and transport modeling. The (major) fractures embedded in the porous matrix are explicitly discretized. Usually, the fractures are resolved with one dimension less than the matrix (e.g. matrix in 3D, fractures in 2D). The fractures have to be characterized by properties like aperture, length, spacing, main orientation. Fractures and matrix are usually coupled at the fracture-matrix interface by flux continuity and continuity of the primary variables (hydraulic head, concentration). This is the most physically-based approach
Random-walk methods
Return to Content