Model output

Highlights
Flow and advective transport mainly in fractures Standard equivalent porous medium model neglects interplay between fractures and matrix Mapping of well capture zones in fractured limestone difficult Plume migration in fractured limestone slows down with time due to matrix diffusion Predictions of different model types differ considerably

Discussion of model concepts Equivalent porous medium (EPM) model The EPM model is the simplest of the considered models and is widely used in practice. Compared to the dual-continuum model or the discrete-fracture model, it has low computational costs. It is well-established for porous media systems without fractures. However, for fractured aquifers, it should only be used for a rough approximation, particularly for solute transport, and has to be used with care. It cannot reproduce the interactions between fractures and matrix (storage in matrix, diffusive mass exchange). That the EPM model fails in heavily fractured limestone aquifers becomes obvious when trying to simulate the tracer tests, which were performed at the Akacievej site. A homogeneous equivalent porous medium model could only be fitted to the fast arrival observed in the tracer tests by lowering the (effective) porosity to very low values (below 1 %, in the order of the fracture porosity). Then, the simulated peak concentrations were higher than the observed ones, because diffusion of tracer into the matrix is neglected by the model. The simulated tracer breakthrough concentration decreased early, and the tailing observed in the field tests could not be reproduced. It is possible to obtain a tailing in the simulated breakthrough curve if a heterogeneous parameter distribution in the porous medium is included (Figure 6.9), introducing very conductive structures and less conductive structures that are less penetrated by flow . However, the variation of the hydraulic conductivity has to be of a similar order of magnitude to the contrast between fracture and matrix conductivity and have a similar connectivity of the highly conductive zones (fractures). Note that a different vertical placement of the screens for injection and extraction can also lead to a tailing in the breakthrough curves. However, this does not account for fracture-matrix interaction and the storage effect of the matrix. The use of an EPM model for the simulation of the migration of a contaminant is not recommended, because exchange processes between fractures and matrix are generally neglected and model results may be misleading for risk assessment or remedial planning. For example, remediation times can be greatly underestimated because the effect of back-diffusion from the matrix cannot be reproduced. It is preferable from the point of view of the actual physics to include fractures in a model as discrete features. Dual-continuum model (DCM) The dual-continuum model matches the observed tracer breakthrough curves from the Akacievej tracer tests better than the EPM model. The fractures and the matrix are each represented as a continuum and the coupling of the two continua allows for an exchange of substances between fractures and matrix. With this model, the breakthrough behavior can be reproduced by fitting the fracture and matrix porosities and conductivities, and the parameters controlling the exchange between fractures and matrix (Dpm, α, a). However, this concept has many degrees of freedom, and it is not clear how to determine the required parameters governing the fracture-matrix exchange experimentally. It is also reported in the literature to be a “black-box” model . The computational effort required to run this model type is usually moderate. It has been reported in the literature that the dual-continuum model has to be recalibrated, when is used to different flow conditions or to different scales. 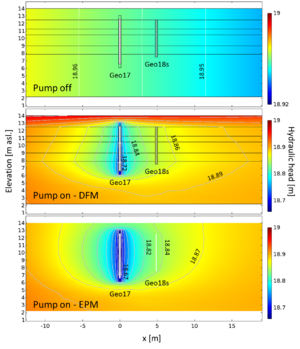Discrete-fracture model (DFM) The discrete-fracture model aims at representing the actual physics and yields the best results. Drawbacks are the often-limited knowledge of the fracture geometry and parameters and the large computational costs. The inclusion of fractures requires a very high grid resolution next to them, and the computational effort does usually not permit to include all fractures in a model. Neglected smaller fractures can be accounted for by increasing the effective diffusion coefficient. The effective diffusion coefficient must be augmented to account for neglected fractures, stagnant flow zones and channeling within the fissures, increasing the diffusive exchange between fractures and matrix . When setting up the model for the tracer tests in Geo18s, Geo19d and Geo5, it was sufficient to include just a few horizontal fractures to provide preferential flow paths for the tracer. The fractures were located to match high-flow zones that were observed on flow logs in the boreholes. The real medium is likely to have many more fractures on different scales, providing a bigger specific surface area for the exchange between fractures and matrix. This can be accounted for by adjusting the matrix diffusivity, which controls the exchange between fractures and matrix. In the simulations presented here, it had to be increased by a factor of 100 to 1000 in order to fit the observed breakthrough behavior. Comparison The tracer tests and model applications have clearly shown that a crucial aspect of the transport of a substance in fractured limestone cannot be reproduced with a simple equivalent porous medium model: the diffusion and back-diffusion of a substance between fractures with strong flow and low-conductive matrix. In a fractured aquifer, this should be accounted for, or the propagation of a substance will not be realistically simulated. Hence, the use of a traditional equivalent porous medium model is not recommended for fractured limestone aquifers. The dual-continuum model can describe the exchange between fractures and matrix while keeping computational efforts low. However, the specification of the exchange terms between fracture and matrix continuum has a crucial influence on the modeling results and a physically-based choice is often challenging. It is not clear how to determine the exchange parameters by measurements. Further, it is questionable if a model, once calibrated, can be employed at a different scale without modifying the used parameters. A requirement for the use of a dual-continuum model is a fracture network with many connected fractures with a relatively uniform distribution, since the fractures are represented as averaged quantities in the fracture continuum. The use of a discrete-fracture model comes with the cost of being the most complex and numerically demanding model described here. However, it represents the actual physics best and can, depending on the knowledge of the fracture system, yields the best results. Usually, only few details about the fracture network are available, which restricts the setup of a detailed model. In this study, the information provided by flow logs could successfully be used to setup a representative network containing the major horizontal flow paths. But such a model does not contain smaller fractures and to compensate for that the diffusion coefficient governing the exchange between fractures and matrix had to be greatly increased. With that, the measured breakthrough curves from the tracer tests could be reproduced. The tracer test in Geo18s before pumping clearly shows that the discrete-fracture model best reproduced the observed data. Since matrix and fractures are both included in the model and the exchange between the two happens naturally (continuity of fluxes, concentrations and heads at the fracture-matrix interface), the discrete-fracture model is the recommended approach in cases where fractures dominate the transport behavior and matrix diffusion occur. Even a simple analytical tool (such as Chambon et al. 2011 ) or a dual-continuum model should be preferred to an equivalent porous medium model, which completely neglects the influence of the fractures. Recommendations for modeling flow and transport in fractured limestone aquifers Integrated modeling approach: combination of modeling, collection of data and field work and update of the conceptual model. Modeling should be included at an early stage of a project based on the available data. This can be used to plan further measurements and investigations. Traditional contaminant transport models fail at reproducing important processes in fractured aquifers (diffusion into matrix and back, slowing down of plume migration speed with time, extent of capture zones) and are not recommended for for fractured limestone geologies similar to the Akacievej site. It is better to use a simple analytical model (as f.e. presented in Chambon, 2011) for the modeling than to use an equivalent porous medium model, which neglects the presence of fractures. In general, it is a good idea to start with a simple model and to increase complexity. If the results look strange, try to simplify the system. Always be critical with modeling results. When a discrete-fracture model is used, the mesh resolution has to be high in the vicinity of the fractures in order to properly approximate the gradients of primary variables there. A too coarse grid resolution can lead to oscillations in the solution and a bad convergence behavior. The mesh resolution is fine enough, when the results do not change when the mesh is further refined. This should be tested to avoid a mesh-dependency of the modeling results. Return to Content